Числа Фибоначчи, как учат в учебниках и как их лучше искать
Одна из первых тем, которой учат в учебниках по программированию — это рекурсия. Это довольно сложная для понимания тема, ну то есть для некоторых (для меня например). И почти в 90% учебников рекурсию рассматривают на примере чисел Фибоначчи.
Числа Фибоначчи — это последовательность чисел, в которой каждое следующее число является суммой двух предыдущих чисел. Начинается последовательность с нуля и единицы (ноль иногда опускают). Выглядит это так:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34… и так до бесконечности
В учебниках нам предлагают найти любой член последовательности зная его номер. Т.е., допустим, нам надо найти шестое число в последовательности. Основная формула для нахождения любого числа выглядит так:
Вот так, примерно, будет выглядеть рекурсия для нахождения n-ного числа:
function fibonacci(n) {
var num;
if (n >= 2) {
num = fibonacci(n - 1) + fibonacci(n - 2);
} else {
num = n
}
return num;
}
alert(fibonacci(6)); // >>> 8
Всё хорошо, функция отлично находит шестое число в последовательности. Но это только пока… Я не знаю насколько мощный у вас комп, но попробуйте найти пятидесятое число:
alert(fibonacci(50));
Уверяю вас, комп ощутимо задумается, если не повиснет в принципе. То есть эта функция — отличный пример рекурсии, и, вместе с тем, отличный пример того, что рекурсия не самый лучший способ решить задачу. Рекурсия очень прожорлива к ресурсам компа, поэтому нужно, по возможности, её избегать.
Итак как же нам найти любое число в последовательности Фибоначчи? Лезем в википедию и узнаём, что нам на помощь приходит формула Бине:
Нас интересует часть до первого знака равенства, реализуем её:
function fibonacci2(n) {
var sq5 = Math.sqrt(5); // сохраняем значение корня из 5, чтобы сэкономить ресурсы
var a = (1 + sq5) / 2;
var b = (1 - sq5) / 2;
return (Math.pow(a, n) - Math.pow(b, n)) / sq5;
}
alert(fibonacci2(500)); // >>> 1.3942322456169767e+104
Как видим новая функция с легкостью вычислила пятисотый член последовательности, что было бы практически нереально для рекурсии.
P.S. Это тоже может быть интересно:
None Found
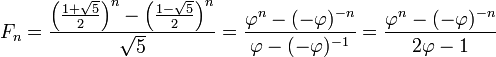
Хм, если запоминать уже посчитанные члены в какой нибудь массив, и проверять на входе в функцию — считали ли мы этот член, то будет тоже быстро. (Правда не зна в js есть массивы или нет, это же javascript?)
Да, в javascript есть массивы. Советую вам изучить этот сайт от корки до корки http://javascript.ru/
Указанный способ чреват потерей точности. Так надёжнее:
return Math.ceil((Math.pow(a, n) — Math.pow(b, n)) / sq5);
Иначе уже на десятом числе спотыкаемся.
Согласен, из-за неточности вычислений с плавающей точкой результат нужно округлять.
return Math.round(((Math.pow(a, n) — Math.pow(b, n)) / Math.sqrt(5)));
так луче потомучто з ceil не точно округляет
Я пока не готов приступить к javascript, а так спасибо!
Вот пример нормальной рекурсии с линейной сложностью (а не с 2 ^ n, как в примере)
function fibonacci(first, second, n)
{
if (n == 0 || n == 1) return n;
if (n == 2) return first + second;
return fibonacci(second, first + second, n — 1);
}
alert(fibonacci(0, 1, 6));
Не Работает ((
Не показывет n’ное число ((
В нормальных учебниках кроме вычисления «в лоб», имеющего сложность O(n^2), приводят еще и простейший алгоритм (хоть рекурсивный, хоть итерационный), имеющий сложность O(n). Суть его в том, что достаточно иметь буфер для двух последних чисел Фибоначчи. Вот простейший итерационный вариант:
function fib(n){
var buf = [0, 1];
var i;
for(i=2; i<=n; i++){
buf[i%2]+=buf[(i+1)%2];
}
return buf[n%2];
}
А если не нравятся остатки от деления, то можно так:
function fib(n){
var buf = [0, 1];
if(n0)buf=[buf[1], buf[0]+buf[1]];
return buf[1];
}
Забавно на сайте, посвященном html/css/javascript, видеть совершенно ученический глюк в обработке символов «меньше» и «больше» (в данном случае было вырезано все, что находилось между этими знаками). Так что посылаю второй вариант еще раз:
function fib(n){
var buf = [0, 1];
if( n 0 )buf=[buf[1], buf[0]+buf[1]];
return buf[1];
}
И вторая попытка закончилась тем же самым. Попытка номер три:
function fib(n){
var buf = [0, 1];
if(n < 0)return n;
while(—n > 0)buf=[buf[1], buf[0]+buf[1]];
return buf[1];
}
Разумеется, в третьей строке функции не n<0, а n<2
А в четвертой строке перед n стоит декремент (два минуса).
Это не глюк, это фича — здесь в комментариях работает простейший HTML (strong, ссылки и т.п.).
1. Если пользователей не предупреждают о такой особенности поведения редактора — это баг.
2. Если знак < за которым следует пробел воспринимается редактором как начало тега — это безусловный баг.
Можно поставить редактор из админки, в нём будет всё что можно и даже больше, но он объёмный, тяжёлый из из-за него происходят тормоза на слабых компах. По крайней мере у нас был такой опыт и люди жаловались, поэтому мы решили поменять его обратно на старый, текущий :(
Можно попробовать ещё раз, посмотрим, что из этого выйдет. Поставил его, проверяйте.
Питонячий код:
def fibo(one,two,n):
if n < 2:
return n
if n == 2:
return one + two
if n > 2:
return fibo(two,one + two,n — 1)
print fibo(1,1,1000)
function count() {
var i = 1;
var a = 2;
var b = 0;
for (i = 1; i < 55;) {
i = i + a;
alert( i );
b = i;
a = a + b;
alert( a );
}
}
count();
Можно ли таким способом?
В смысле, простым циклом, а не рекурсией? Можно, конечно (только условие выхода из цикла лучше бы передавать параметром, а не хардкодить:). Но по формуле даже при не очень большом n получается эффективнее, даже без «экономии ресурсов».