Перевод статьи Transforms on SVG Elements с сайта css-tricks.com, автор — Ана Тудор.

Перед вами гостевой пост Аны Тудор. Ана всегда проделывает грандиозную работу, погружаясь в математику, стоящуя за тем, что мы можем делать графически в вебе. В данном случае, это очень кстати, поскольку есть несколько способов работы с SVG-трансформациями и они требуют немного математического мышления, особенно для преобразования одного типа в другой для наилучшей кроссбраузерной поддержки. Давай, Ана.

Как и HTML-элементами, SVG-элементами можно управлять при помощи функций для трансформации. Однако, далеко не всё работает с SVG-элементами так, как с HTML-элементами

Для начала, CSS-трансформации для SVG-элементов не работают в IE. Конечно, есть вариант с использованием SVG-атрибутов трансформации для IE, в случае, если нам нужно применять для наших элементов только 2D-трансформации.

Однако, в этом случае, все параметры для функций трансформаций представлены в виде чисел, что означает, что мы не можем управлять единицами измерения и комбинировать их. Например, мы не можем использовать значения в % для функций сдвига (хотя значения % всё равно бы не стали работать для CSS-трансформаций в Firefox, и не важно, говорим ли мы о значениях transform-origin или параметрах translate()), и все значения для поворота или угла наклона высчитываются в градусах, поэтому мы не можем применять другие единицы измерения, которые доступны в CSS.

Еще одна проблема — тот факт, что определение возможностей скриптом не справляется (чтение значения CSS-трансформации при помощи JS вернёт матрицу, эквивалентную трансформации, которую мы установили в нашей таблице стилей), поэтому нам нужен либо другой способ проверки для IE, либо нам надо повсеместно использовать атрибуты трансформации (что в каком-то смысле кажется более легким путем вообще)

Главная разница в работе между HTML- и SVG-элементами — локальная система координат элемента. У каждого элемента, будь то HTML- или SVG-элемент, есть такая система. Для HTML-элементов эта система координат начинается в точке 50% 50% элемента. Для SVG-элементов (если мы не применяли трансформации к элементу или его предкам в пределах элемента <svg>) исходная точка находится в 0 0 SVG-холста. Это приведёт к разным результатам с трансформациями rotate, scale или skew, если точка 50% 50% SVG-элемента не совпадает с точкой 0 0 SVG-холста.

Чтобы лучше это понимать, давайте посмотрим, как работают функции трансформации.

Как работают функции трансформации

Единственное, что нам надо понимать о трансформациях, это то, что их эффект накапливается при применении к вложенным элементам. Это означает, что трансформации, применённые к элементам с потомками, также повлияют на всех потомков вместе с их системой координат и на результат любых трансформаций на этих потомках. Чтобы было проще, будем считать, что в следующих случаях у наших элементов нет никаких родительских элементов с трансформациями, которые к ним применены. И также будет считать, что у наших элементов нет никаких потомков.

Сдвиг

Сдвиг перемещает все точки элемента в том же направлении и на ту же величину. Сдвиг сохраняет параллельность, углы и расстояния. Это можно интерпретировать, как сдвиг начальной точки системы координат элемента — когда это происходит, любой элемент, положение которого описывается относительно этой начальной точки (сам элемент и любые его потомки), тоже сдвигается. Его результат не зависит от положения системы координат.

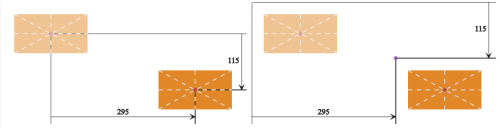Рисунок 1: трансформация сдвига: HTML-элементы (слева) напротив SVG-элементов (справа)

На рисунке выше представлено сравнение примеров с HTML (слева) и SVG (справа). Полупрозрачные рисунки элементов — это их исходное положение (до применения сдвига). Трансформация сдвига перемещает элементы вместе с их системами координат, и это же произойдет с любыми потомками наших элементов, если таковые будут.

Как вы уже знаете, различие между двумя случаями — положение системы координат. В случае с HTML, начало координат находится в точке 50% 50% элемента. В случае с SVG начало координат располагается в точке 0 0 холста (если мы не применяли трансформации ни к каким возможным предкам элемента в пределах элемента <svg>). Тем не менее, при сдвиге положение системы координат относительно элемента не влияет на конечное положение элемента.

Как для HTML-, так и для SVG-элементов, при использовании CSS-трансформации у нас есть три функции для сдвига, доступные для 2D: translateX(tx), translateY(ty) и translate(tx[, ty]). Первые две влияют только на направления x и y (как указано системой координат элемента), соответственно. Заметьте, что если другая трансформация применена до сдвига, то направления x и y, возможно, больше не будут горизонтальным и вертикальным, соответственно. Третья функция сдвига перемещает элемент на tx вдоль оси x и на ty вдоль оси y. Параметр ty необязательный, и если он не указан, по умолчанию он равен нулю.

SVG-элементы могут также перемещаться при помощи атрибутов для трансформации. В этом случае, у нас есть только функция translate(tx[ ty]).  Здесь значения могут разделяться пробелами, а не только запятыми, как в аналогичной функции CSS-трансформации. Поэтому в очень простом случае, когда 1 в пользовательской системе координат SVG равно 1px, это равнозначно 1px, следующие два способа сдвига SVG-элемента равнозначны:

• применение CSS-трансформации:

rect {
  /* не работает в IE */
  transform: translate(295px,115px);
}

• применение атрибутов для SVG-атрибута для трансформации:

<!— работает везде-->
<rect width='150' height='80' transform='translate(295 115)' />

Заметьте: SVG-атрибут для трансформации и CSS-свойство для трансформации будут объединены.

Последовательные трансформации translate() можно складывать, это значит, что цепочки вида translate(tx1, ty1) translate(tx2, ty2) можно записывать как translate(tx1 + tx2, ty1 + ty2). Заметьте, что это верно, если в цепочке трансформаций между ними не стоит трансформации другого типа. Обратный сдвиг translate(tx, ty) делается при помощи другого сдвига translate(-tx, -ty).

Поворот

2D-поворот перемещает элемент и любые его потомки, если они есть, вокруг фиксированной точки (точки, положение которой сохраняется, следуя за трансформацией). Конечный результат зависит от положения этой фиксированной точки. Два поворота на один и тот же угол вокруг двух разных точек приведут к разным результатам. Так же, как и сдвиг, поворот не деформирует элемент и сохраняет параллельность, углы и расстояния. Последовательные трансформации rotate() вокруг той же фиксированной точки складываются, как и в случае со сдвигом. Поворот в обратную сторону делается при помощи другого поворота на тот же угол в обратном направлении вокруг той же самой точки.

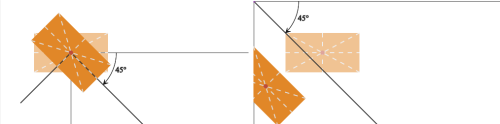Рисунок 2: базовая трансформация поворота: HTML-элементы (слева) напротив SVG-элементов (справа)

На рисунке выше представлено сравнение примеров с HTML (слева) и SVG (справа). Полупрозрачные рисунки элементов — это их исходное положение (до применения поворота). Поворот перемещает элементы и их системы координат вокруг фиксированного начала координат, и это же произойдет с любыми потомками наших элементов, если таковые будут.

В случае с HTML, начальная точка системы координат элемента находится в 50% 50% элемента, поэтому все поворачивается вокруг этой точки. Однако, в случае с SVG, исходная точка находится в 0 0 SVG-холста (если мы не применяли трансформации ни к каким возможным предкам элемента в пределах элемента <svg>), в результате чего всё будет перемещаться вокруг этой точки.

Для CSS-трансформаций функция 2D-поворота довольно простая: только rotate(angle). Значение angle может быть представлено в градусах (deg), радианах (rad), оборотах (turn) или градах (grad). Также мы можем использовать значение calc() (например, что-нибудь типа calc(.25turn - 30deg)), но на данный момент это работает только в Chrome 38+/ Opera. Если вы используете положительное значение угла, тогда поворот будет идти по часовой стрелке (и наоборот, при отрицательном значении угла, поворот будет идти против часовой стрелки).

В случае с атрибутами для SVG-трансформации, функция поворота немного отличается — rotate(angle[ x y]). Значение angle работает аналогичным с функцией CSS-трансформации способом (положительное значение означает поворот по часовой стрелке, отрицательное значение — против часовой), но значение градусов должно быть безрамерным. Необязательные безразмерные параметры x и y указывают координаты фиксированной точки, вокруг которой мы поворачиваем элемент (и его систему координат). Если они опущены, тогда фиксированной точкой будет начальная точка системы координат. Если указать только параметры angle и x, значение будет невалидным и трансформация не применится.

Как и в функции translate(), параметры могут разделяться пробелами или запятыми.

Заметьте, что наличие параметров x и y не означает, что начальная точка системы координат переместится в эту точку. Система координат, как и сам элемент (и любые потомки, если они есть) просто будут вращаться вокруг точки x y.

Это означает, что у нас есть два равнозначных способа поворота SVG-элемента (результат можно увидеть справа на предыдущем рисунке):

• применение CSS-трансформации:

rect {
  /* не работает в IE */
  transform: rotate(45deg);
}

• применение атрибута для SVG-трансформации:

<!-- работает везде -->
<rect x='65' y='65' width='150' height='80' transform='rotate(45)' />

Также в CSS мы можем указать значение transform-origin, чтобы сымитировать применение параметров x и y. Значения длины указываются относительно системы координат элемента, а процентные значения — относительно самого элемента, поэтому они, кажется, идеальны для того, что мы хотели получить. Однако, нам надо учитывать две вещи.

Во-первых, CSS transform-origin и фиксированная точка, указанная в функции rotate() — не одно и тоже. В качестве очень простого примера, скажем, возьмем всего лишь поворот вокруг точки 50% 50% в SVG, не столь важно. Рассмотрим два случая:

rect {
  transform: rotate(45deg);
  transform-origin: 50% 50%;
}

<rect x='65' y='65' width='150' height='80' 
transform='rotate(45 140 105)' />
<!-- 140 = 65 + 150/2 -->
<!-- 105 = 65 +  80/2 -->

В обоих случаях элемент должен поворачиваться одинаково (должен, если поддерживается браузером, но это уже другая история), как видно на следующем рисунке:

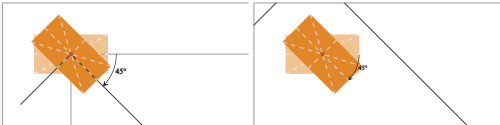Рисунок 3: вращение SVG-элемента вокруг установленной точки: применение CSS (слева) и атрибута для SVG-трансформации (справа)

Это показывает разницу между ними. При использовании CSS, система координат элемента сначала перемещается от точки 0 0 SVG-холста в точку 50% 50% элемента. Затем элемент поворачивается. При использовании атрибута для SVG-трансформации, элемент и его система координат просто поворачивается вокруг точки, указанной во втором и третьем аргументе функции rotate(), точки, координаты которой мы вычислили так, чтобы она находилась в точке 50% 50% элемента. Начальная точка системы координат элемента по-прежнему находится снаружи элемента, и эта начальная точка будет влиять на любые последующие трансформации, зависящие от неё.

Чтобы лучше это понять, давайте укажем другой поворот (сразу после первого), который поворачивает элемент на 45° в противоположном направлении:

rect {
  transform: rotate(45deg) rotate(-45deg);
  transform-origin: 50% 50%;
}

<rect x='65' y='65' width='150' height='80' 
transform='rotate(45 140 105) rotate(-45)' />
<!-- 140 = 65 + 150/2 -->
<!-- 105 = 65 +  80/2 -->

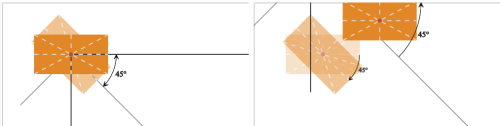Рисунок 4: цепочка поворотов для SVG-элемента: CSS-трансформации (слева) и атрибут для SVG-трансформации (справа)

Как показано на рисунке выше, при использовании CSS-трансформации и установке transform-origin в 50% 50%, два поворота компенсируют друг друга, но при использовании SVG-атрибута transform, фиксированная точка, вокруг которой мы поворачиваем элемент, различается между двумя поворотами — она является точкой 50% 50% элемента для первого поворота и начальной точкой системы координат элемента для второго. В этой ситуации поворот в обратную сторону делается легко; просто используйте rotate(-45 140 105) вместо rotate(-45).

Однако, это не отменяет того факта, что у нас есть только один transform-origin (поскольку у системы координат элемента есть только одна начальная точка), но при использовании SVG-атрибута transform, мы можем применять множественные повороты, каждый из которых поворачивает элемент вокруг разной точки. Поэтому, если мы хотим сначала повернуть наш прямоугольник на 90° вокруг его нижнего правого угла, а затем ещё на 90° вокруг его верхнего правого угла, то это легко сделать при помощи атрибута для SVG-трансформации — мы просто указываем разные фиксированные точки для каждого поворота.

<rect x='0' y='80' width='150' height='80' 
transform='rotate(90 150 160) rotate(90 150 80)'/>
<!--
bottom right:
  x = x-offset + width = 0 + 150 = 150
  y = y-offset + height = 80 + 80 = 160
top right:
  x = x-offset + width = 0 + 150 = 150
  y = y-offset = 80
-->

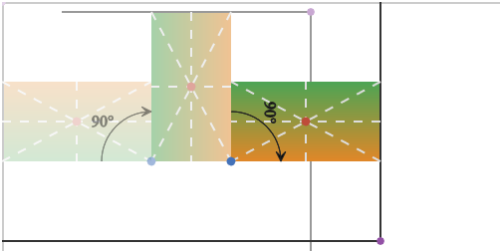Рисунок 5: цепочка поворотов вокруг разных фиксированных точек (атрибут для SVG-трансформации)

Но как нам получить тот же самый эффект при помощи CSS-трансформаций? Это легко сделать для первого поворота, поскольку можно установить transform-origin в right bottom, но как быть со вторым поворотом? Если дописать его в CSS-правиле после первого, то он просто повернёт элемент ещё на 90° вокруг той же самой точки (right bottom).

Нам нужно три сцепленных трансформации, для того, чтобы поворот элемента вокруг фиксированной точки не зависел от того, где находится его transform-origin. Во-первых, это трансформация translate(x, y), которая переместит начальную точку системы координат элемента таким образом, чтобы она совпадала с фиксированной точкой, вокруг которой мы хотим всё поворачивать. Во-вторых, это сам поворот. И наконец, в-третьих, это translate(-x, -y) — противоположность первому сдвигу.

В этом случае наш код мог бы быть таким:

rect {
  transform-origin: right bottom; /* или 100% 100%, что одно и тоже */
  transform:
    rotate(90deg)
    translate(0, -100%) /* идём от нижнего правого до верхнего правого края */
    rotate(90deg)
    translate(0, 100%);
}

На нижнем рисунке показано, как это работает, шаг за шагом:

Рисунок 6: иллюстрация того, как работает цепочка CSS-трансформаций

Вторая проблема с transform-origin, это то, что в Firefox работают только значения длины. Процентные значения и ключевые слова — нет, поэтому нам придется заменять их значениями длины. И процентные значения внутри трансформаций translate(), также не работают в Firefox.

Масштабирование

Масштабирование изменяет расстояние от начала координат элемента до любой точки элемента (и любых потомков, если таковые есть) на тот же коэффициент в указанном направлении. Если коэффициент не одинаковый во всех направлениях — в случае чего получается равномерное масштабирование — форма элемента не сохраняется.

Коэффициент масштабирования в диапазоне (-1, 1) уменьшает элемент, тогда как коэффициент вне этого диапазона увеличивает его. Отрицательный коэффициент масштабирования также отражает элемент центрально-симметрично относительно его начала координат, в дополнение к изменению размера. Если только один коэффициент масштабирования отличается от 1, то получается масштабирование по одной оси.

Результат трансформации масштаба зависит от положения начальной точки системы координат. Две трансформации масштабирования с одним и тем же коэффициентом на одном и том же элементе дадут разный результат при разном положении начала координат.

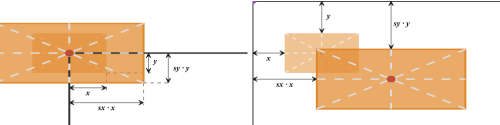Рисунок 7: трансформация масштабирования: HTML-элементы (слева) и SVG-элементы (справа)

На рисунке выше представлено сравнение примеров с HTML (слева) и SVG (справа). В обоих случаях мы масштабируем элемент, используя коэффициент масштабирования sx вдоль оси x и sy вдоль оси y. Разница в положении начальной точки системы координат элемента, которая в случае с HTML находится в точке 50% 50% элемента, а в случае с SVG в точке 0 0 SVG-холста (если мы не применяли трансформации ни к каким возможным предкам элемента в пределах элемента <svg>).

При использовании CSS-трансформаций у нас есть три функции масштабирования, которые доступны для 2D-трансформаций: scale(sx[, sy]), scaleX(sx) и scaleY(sy). Первая функция масштабирует элемент на sx вдоль оси x и на sy вдоль оси y. Параметр sy необязательный, и если он не указан, то предполагается, что он равен sx, делая таким образом масштабирование одинаковым во всех направлениях. sx и sy всегда являются безразмерными значениями. Другие две функции действуют только в направлениях x и y (как указано системой координат элемента), соответственно. scaleX(sx) равнозначно scale(sx, 1) или просто scale(sx), а scaleY(sy) равнозначно scale(1, sy). Если другая трансформация применяется до масштабирования, направления x и y могут уже не быть горизонтальным и вертикальным, соответственно.

В случае с атрибутами для SVG-трансформации у нас есть только функция scale(sx[ sy]). Снова, значения здесь могут разделяться пробелами, а не только запятыми, как в аналогичной функции CSS-трансформации.

Поэтому для SVG-элементов следующие два метода масштабирования равнозначны:

• применение CSS-трансформации

rect {
  /* не работает в IE */
  transform: scale(2, 1.5);
}

• применение атрибута для SVG-трансформации

<!-- работает везде -->
<rect x='65' y='65' width='150' height='80' transform='scale(2 1.5)' />

Эти функции приводят к одинаковому результату, как показано в правой части рисунка 7. Но что, если мы хотим получить тот же самый эффект, который мы получаем при применении той же функции масштабирования для HTML-элемента? Ну, мы можем делать это также, как и в поворотах.

С CSS-трансформациями у нас есть выбор: либо задать нашему SVG-элементу правильный transform-origin, либо добавить в цепочку трансформаций сдвиги до и после масштабирования — сначала мы сдвигаем систему координат так, что ее начало оказывается в точке 50% 50% нашего SVG-элемента, затем масштабируем, а затем обращаем первый сдвиг. С SVG-атрибутом transform у нас есть только вариант с цепочкой трансформаций. Так что код для вышеописанного случая был бы таким:

• Применение CSS-трансформации при помощи transform-origin

rect {
  /* не работает в IE */
  transform: scale(2, 1.5);

  /* не работает в Firefox, если мы только не заменим значения % на значения с абсолютной длиной */
  transform-origin: 50% 50%;
}

• Применение цепочки CSS-трансформаций

rect {
  /* не работает в IE */
  transform: translate(140px, 105px)
  scale(2 1.5)
  translate(-140px, -105px);
}

• Применение функций цепочки трансформаций в виде значения для атрибута SVG-трансформации

<rect x='65' y='65' width='150' height='80' 
transform='translate(140 105) scale(2 1.5) translate(-140 -105)'/>
<!-- работает везде -->

Следующий демо-пример иллюстрирует, как работает метод с цепочкой трансформаций (нажмите кнопку «воспроизведение» (►) для старта):

See the Pen Chaining on SVG elements to scale wrt a certain point by Максим (@psywalker) on CodePen.

Что ещё нужно помнить о масштабировании — это что две последовательные трансформации scale() (scale(sx1, sy1) scale(sx2, sy2)) могут быть записаны как scale(sx1*sx2, sy1*sy2), а обратная трансформация делается при помощи scale(1/sx1, 1/sy1). Если все коэффициенты масштаба по модулю равны 1, то такое масштабирование — само себе обратная трансформация.

Наклон

Наклон элемента вдоль оси смещает каждую из его точек (кроме тех, которые находятся точно на оси наклона) в этом направлении на ту величину, которая зависит от угла наклона и расстояния между этой точкой и осью наклона. Это значит, что изменяется только координата вдоль оси наклона, а координата вдоль другой оси остаётся неизменной. В отличие от поворота, наклон деформирует элемент, превращая квадраты в неравносторонние параллелограммы, а круги в эллипсы. Наклон не сохраняет углы (при наклоне на угол α 90-градусные углы прямоугольного элемента становятся 90° ± α) или длина любого сегмента не параллельна оси наклона. Однако, площадь элемента сохраняется.

В отличие от сдвига или поворота, наклоны не складываются. Наклон элемента вдоль оси на угол α1, а затем наклон снова вдоль той же оси на другой угол α2 — не то же самое, что наклон элемента вдоль этой оси на угол α1 + α2.

Демо-пример ниже показывает, как работает наклон — изменяйте угол и/или ось, чтобы увидеть, как это влияет на исходный квадрат.

See the Pen How the skew transform works by Ana Tudor (@thebabydino) on CodePen.

Угол наклона — это угол между конечным и исходным положением оси, которая изменяется после применения трансформации (а не оси, вдоль которой мы наклоняем элемент). Положительный угол наклона в интервале [0°, 90°] добавляет значение того же знака, что у неизменной координаты, к исходному значению меняющейся координаты, которая изменилась (координата вдоль угла наклона), а отрицательное значение в интервале [-90°, 0°] добавляет значение, знак которого является противоположным этой фиксированной координаты.

Если мы делаем наклон вдоль оси x, то для любой точки нашего элемента координата y этой точки остаётся такой же, а координата x изменяется на величину d в зависимости от угла наклона и от фиксированной координаты y (где-то на 15-й минуте этого доклада поясняется, как величина d может быть вычислена). Верхняя и нижняя стороны (и любой другой сегмент, параллельный оси x) остаются той же длины, а левая и правая стороны становятся длиннее по мере увеличения угла наклона, уходя в бесконечность в случае угла ±90°. Как только это значение превышается, они начитают становиться короче, пока мы не получим угол в ±180°.

Заметьте, что результат наклона на угол в интервале (90°, 180°] равнозначен результату наклона на угол α - 180°> (который в конечном итоге оказался бы в интервале (-90°, 0°]). Также результат наклона на угол в интервале (-180°, -90°] равнозначен результату наклона на угол — α + 180° (который в конечном итоге оказался бы в интервале [0°, 90°))

Если мы делаем наклон вдоль оси y, то координата x остаётся такой же для любой точки нашего элемента, а координата y изменяется на величину d в зависимости от угла наклона и от фиксированной координаты x. Правая и левая стороны (и любой другой сегмент, параллельный оси y) остаются той же длины, а верхняя и нижняя стороны становятся длиннее по мере увеличения угла наклона, уходя в бесконечность в случае угла ±90°. Как только это значение превышается, они начитают становиться короче, пока мы не получим угол в ±180°.

Так же, как в масштабировании, результат действия наклона зависит от положения изначальной точки системы координат элемента. Две трансформации масштабирования с одним и тем же коэффициентом на одном и том же элементе дадут разный результат при разном положении начала координат. Две трансформации наклона на тот же самый угол вдоль той же самой оси приведут к разным результатам при разном положении начала координат.

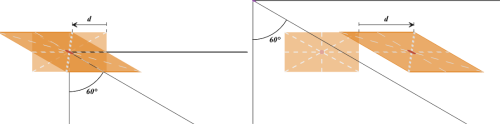Рисунок 8: трансформация наклона: HTML-элементы (слева) и SVG-элементы (справа)

На рисунке выше представлено сравнение примеров с HTML (слева) и SVG (справа). В обоих случаях, мы наклоняем наши элементы вдоль оси x на тот же угол наклона. Разница в положении начальной точки системы координат элемента, которая в случае с HTML находится в точке 50% 50% элемента, а в случае с SVG в точке 0 0 SVG-холста (если мы не применяли трансформации ни к каким возможным предкам элемента в пределах элемента <svg> в случае с SVG).

Для простоты, давайте сосредоточимся на том, что случается только с одной точкой наших элементов: верхний правый угол. В обоих случаях координата y сохраняет своё положение — точка не двигается по вертикали, только по горизонтали. Однако, в случае HTML мы видим, что по горизонтали этот угол двигается влево (в отрицательном направлении оси x), а в случае с SVG вправо. А нижний правый угол двигается вправо, по мере наклона, как в HTML, так и в случае с SVG. Итак, как это работает?

Ну, как упоминалось выше, при наклоне вдоль оси x, координата y любой точки остаётся такой же, хотя к исходной точке координаты x той же точки мы добавляем величину d, которая зависит от угла наклона и от фиксированной координаты y. Эта величина d совпадает по знаку с фиксированной координатой y, если угол наклона находится в интервале [0°, 90°], и противоположна ей по знаку, если угол наклона находится в интервале [-90°, 0°].

В обоих случаях наш угол 60°, поэтому дело решает знак координаты y верхнего правого угла. В случае с HTML начальная точка системы координат элемента находится в точке 50% 50% элемента, координата y верхнего правого угла элемента является отрицательной, поскольку ось y направлена вниз. Однако, в случае с SVG, где начальная точка системы координат элемента находится в точке 0 0 SVG-холста, координата y верхнего правого угла элемента положительна. Это означает, что в случае с HTML мы добавляем отрицательную величину к исходной точке координаты x верхнего правого угла, заставляя его двигаться влево, а в случае с SVG мы добавляем положительную величину к исходной координате x верхнего правого угла, заставляя его двигаться вправо.

Независимо от того, наклоняем ли мы SVG-элемент при помощи CSS-трансформаций или атрибута для SVG-трансформации, нам доступны две функции: skewX(angle) и skewY(angle). Первая функция наклоняет элемент вдоль оси x, а вторая наклоняет его вдоль оси y.

В CSS-трансформациях значение angle указывается с единицей измерения. Оно может быть представлено в градусах (deg), радианах (rad), оборотах (turn), градах (grad) или даже в виде calc(), чтобы комбинировать любые эти единицы измерения (но имейте ввиду, что на данный момент calc() с единицами измерения для угла работает только в браузерах на движке Blink)

При наклоне элемента с помощью атрибута для SVG-трансформации наше значение angle всегда представляет безразмерное значение градусов.

Это означает, что у нас есть два равнозначных способа наклона SVG-элемента (результат можно видеть на предыдущем рисунке справа):

• использование CSS-трансформаций:

rect {
  transform: skewX(60deg); /* не работает в IE */
}

• использование атрибута для SVG-трансформации:

<!-- работает везде -->
<rect x='65' y='65' width='150' height='80' transform='skewX(60)' />

Если вы хотите получить тот же самый эффект, который мы получаем при применении аналогичной функции наклона для  HTML-элемента, то для этого у нас есть три способа, как и при масштабировании:

• использование CSS-трансформации при помощи transform-origin

rect {
  /* не работает в IE */
  transform: skewX(60deg);
  /* не работает в Firefox, если мы только не заменим значения % на значения с абсолютной длиной */
  transform-origin: 50% 50%;
}

• использование цепочки CSS-трансформаций

rect {
  /* не работает в IE */
  transform: translate(140px, 105px)
  skewX(60deg)
  translate(-140px, -105px);
}

• использование цепочки функций трансформации в виде значения атрибута для SVG-трансформации:

<!-- работает везде -->
<rect x='65' y='65' width='150' height='80' 
transform='translate(140 105) skewX(60) translate(-140 -105)' />

Следующий демо-пример иллюстрирует как работает «цепочный» метод:

See the Pen Chaining on SVG elements to skew wrt a certain point by Ana Tudor (@thebabydino) on CodePen.

Сокращение цепочки

Всё в порядке, цепочки трансформаций делают своё дело. Можно поворачивать, масштабировать и наклонять SVG-элементы, и они ведут себя так же, как вели бы и HTML-элементы при тех же самых трансформациях. А если мы применяем цепочку трансформаций в виде значения для SVG-атрибута, то у нас даже есть возможность получить желаемый результат в IE. Но это уродство! Неужели нет более простого способа сделать это?

Ну, если мы начнём с нашего SVG-прямоугольника, точка 50% 50% которого находится в точке 0 0 SVG-холста, то мы можем «вырезать» один сдвиг в нашей цепочке, сокращая наш код поворота:

<rect x='-75' y='-40' width='150' height='80' 
transform='translate(140 105) rotate(45)'/>
<!-- 75 = 150/2, 40 = 80/2 -->

See the Pen Chaining on SVG elements to rotate wrt a certain point #1 by Ana Tudor (@thebabydino) on CodePen.

Мы также могли бы избавиться от первого сдвига при помощи правильно подобранного атрибута viewBox для элемента <svg>, содержащего наш прямоугольник. У атрибута viewBox есть четыре значения, которые разделены пробелом. Первые два указывают координаты x и y верхнего левого угла SVG-холста в пользовательских единицах измерения, а другие две указывают его width и height в пользовательских единицах измерения. Если атрибут viewBox не указан, то координаты верхнего левого угла будут 0 0.

Ниже можно увидеть разницу между элементом <svg>, у которого не указан viewBox, и элементом <svg> с viewBox='-140 -105 280 210':

Рисунок 9: Элемент <svg>, у которого не указан атрибут viewBox, и элемент <svg> с viewBox

Возвращаясь к нашему примеру, если мы установим viewBox так, чтобы точка 0 0 SVG-холста разместилась там, где у нас находится точка 50% 50% нашего прямоугольника, то наш код станет таким:

<svg viewBox='-140 -105 650 350'>
<rect x='-75' y='-40' width='150' height='80' transform='rotate(45)'/>
</svg>

See the Pen Setting proper `viewBox` to rotate wrt a certain point #1 by Ana Tudor (@thebabydino) on CodePen.

Практическое применение

Размещение точки 0 0 нашего SVG-холста и любого другого желаемого элемента прямо в середине облегчает работу с трансформациями, потому что в этом случае точка 0 0 SVG-холста совпадает с точкой 50% 50% элемента, который мы хотим трансформировать. Следующий демо-пример (жмите воспроизведение/пауза) показывает три четырёхконечные звёзды, которые изначально расположены в середине, а затем повёрнуты, смещены, наклонены и сжаты без необходимости в установке transform-origin или в добавлении сдвигов в цепочке:

See the Pen SVG Stars — final by Ana Tudor (@thebabydino) on CodePen.

Давайте рассмотрим, как работает это демо шаг за шагом.

Создается звезда очень легко — простой многоугольник с восемью точками. Демо-пример ниже показывает, как они позиционируются относительно начальной точки (0 0) SVG-холста. Наводите мышкой на пары x,y в коде или на сами точки, чтобы увидеть что чему соответствует.

See the Pen 4 point star — the points by Ana Tudor (@thebabydino) on CodePen.

У нас есть три таких звезды. Мы не будем повторять код для многоугольника три раза, а просто положим его в элемент <defs>, а затем трижды используем его в элементе <use>.

<svg viewBox='-512 -512 1024 1024'>
  <defs>
    <polygon id='star' points='250,0 64,64 0,250 -64,64 -250,0   -64,-64 0,-250 64,-64'/>
  </defs>
  <g>
    <use xlink:href='#star'/>
    <use xlink:href='#star'/>
    <use xlink:href='#star'/>
  </g>
</svg>

Первое, что мы сделаем, это отмасштабируем наши звёзды от 0 до 1:

use {
  animation: ani 4s linear infinite;
}
@keyframes ani {
  0% { transform: scale(0); }
  25%, 100% { transform: scale(1); }
}

Это даст нам следующий результат:

See the Pen SVG Stars — step #1 by Ana Tudor (@thebabydino) on CodePen.

Следующее, что мы хотим сделать, это добавить поворот к нашей покадровой анимации. Но нам нужен разный поворот для каждой звезды — допустим, случайный угол плюс определённый угол, рассчитываемый по порядковому номеру звезды. Это означает, что мы не можем применить одну и ту же покадровую анимацию для всех трёх звёзд; нам нужно три разных анимации. Также это поможет нам сделать заливку разной.

$n: 3;
$?: 360deg/$n;
$?: random($?/1deg)*1deg;

@for $i from 1 through $n {
  $?: $? + ($i - 1)*$?;
  
  use:nth-of-type(#{$i}) {
    fill: hsl($?, 100%, 80%);
    animation: ani-#{$i} 4s linear infinite;
  }

  @keyframes ani-#{$i} {
    0% { transform: scale(0); }
    25% { transform: scale(1); }
    50%, 100% { transform: rotate($?); }
  }

}

Вы можете посмотреть результат в коде ниже:

See the Pen SVG Stars — step #2 by Ana Tudor (@thebabydino) on CodePen.

Следующим шагом будет сдвиг и масштабирование нашей звезды:

@keyframes ani-#{$i} {
  0% { transform: scale(0); }
  25% { transform: scale(1); }
  50% { transform: rotate($?); }
  75%, 100% {
    transform: rotate($?) translate(13em) scale(.2);
  }
}

See the Pen SVG Stars — step #3 by Ana Tudor (@thebabydino) on CodePen.

Мы почти у цели! Нам просто надо наклонить звёзды и применить трансформацию для масштабирования, чтобы подправить их размеры после наклона.

@keyframes ani-#{$i} {
  0% { transform: scale(0); }
  25% { transform: scale(1); }
   50% { transform: rotate($?); }
  75% {
    transform: rotate($?) translate(13em) scale(.2);
}
  83% {
    transform: rotate($?) translate(13em) scale(.2)
      skewY(30deg) scaleX(.866);
  }

  91% {
    transform: rotate($?) translate(13em) scale(.2)
    skewY(60deg) scaleX(.5);
  }

  100% {
    transform: rotate($?) translate(13em) scale(.2)
    skewY(90deg) scaleX(0);
  }
}

Здесь я добавила больше одного ключевого кадра для точности. В то время как угол наклона изменяется линейно, корректирующий коэффициент масштаба — нелинейно, его значение — это косинус угла наклона, и как видно на следующем изображении, график функции косинуса между 0° и 90° — не прямая.

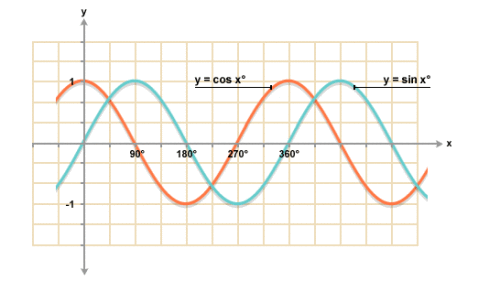Рисунок 10: график синуса (синий) и косинуса (красный)

Однако, этот пример на чистом CSS немного глючит в Firefox и не работает ни в каком IE, поскольку ни одна из версий IE не поддерживает CSS-трансформации для SVG-элементов. Всё это можно исправить, если использовать атрибуты для SVG-трансформации и анимировать их значения при помощи JavaScript. Вы можете посмотреть JavaScript-версию ниже (нажмите, чтобы запустить).

See the Pen Stars — JS version by Ana Tudor (@thebabydino) on CodePen.

P.S. Это тоже может быть интересно:

• Тёмная сторона CSS: выходим за рамки и взрываем звезды с border-image и градиентами
• CSS-выражения от контейнера для дизайнеров
• Псевдокласс :has() — не только «родительский селектор»